I'm currently a Postdoctoral research associate at the Department of Astrophysical Sciences at Princeton University.
My research interests include High Performance Computing, Parallel and GPU computing, Computational Fluid Dynamics and
Planet formation, with emphasis in planet-disc interaction.
Recent Work
Spectral Difference method with a posteriori limiting: Application to the Euler equations in one and two space dimensions
Read | arXiv
In this work, we have presented a novel implementation of an arbitrarily high-order SD method, with a second order FV solver as fallback scheme. We have demonstrated that the resulting method has robust shock-capturing capabilities.
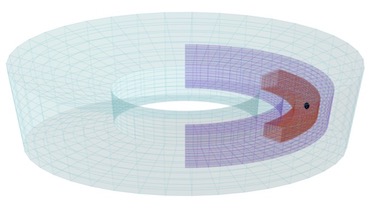
Eccentricity driving of pebble accreting low-mass planets
Read | arXiv
We have adapted our nested-meshes version of the fargo3d code to perform simulations of a freely evolving,
luminous planet in a thermally diffusive gaseous disc around a solar-mass star. The implementation allowed
us to improve the resolution of previous work (Eklund & Masset 2017), and to get converged results for the
eccentricity reached at larger time, or asymptotic eccentricity, by a low-mass planet as a function of its luminosity.
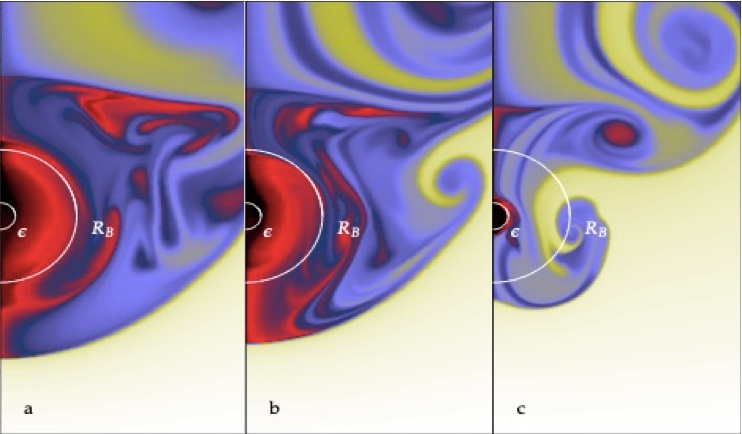
Dynamical friction with radiative feedback–II. High-resolution study of the subsonic regime
Read | arXiv
We have performed high-resolution simulations in the subsonic regime in two and three dimensions that resolve the Bondi radius of a perturber
travelling at constant speed in a gas with initially uniform density and temperature. We have found that for perturbers with sufficiently small
mass, the net force is in agreement with that obtained from linear theory (Masset & Velasco-Romero 2017). At larger masses, the thermal forces are smaller than those given by
linear theory.
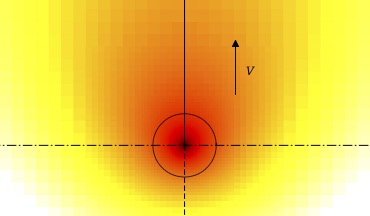
Numerical study of dynamical friction with thermal effects–I. Comparison to linear theory
Read | arXiv
We have conducted extensive numerical simulations in order to check the impact of thermal effects on the dynamical friction on to a massive perturber,
both with and without intrinsic luminosity (i.e. with or without radiative feedback). Owing to the wide interval of length scales required to capture
accurately thermal effects, we had to resort to nested meshes, that we implemented in the GPU version of the FARGO3D code.
Gallery

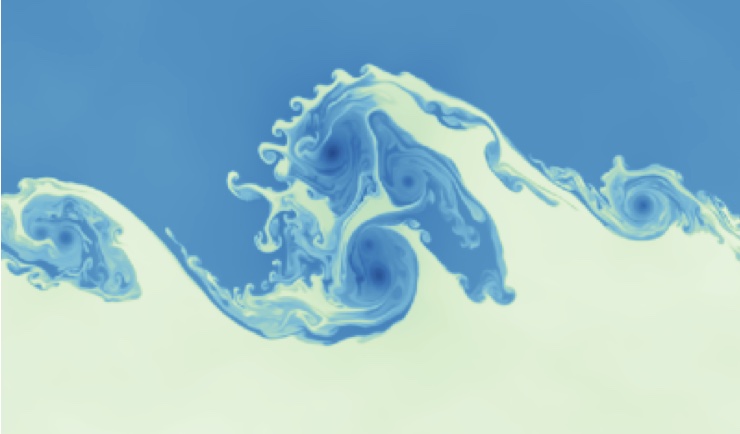
Kelvin–Helmholtz instability: SD 4th order, 512x512 elements
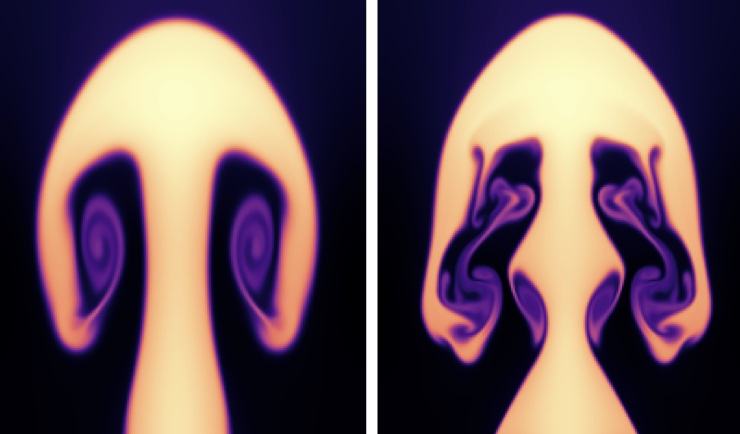
Rayleigh–Taylor instability: Godunov 2nd-order, 512, 1024, 2048 and 4096 cells

Turbulent Convection: SD 4th order, 512x1024 DOF

Dynamical Friction: FARGO3D+NM
Movies
Kelvin–Helmholtz instability: Density map obtained with our Spectral-Differences code for 512x512 elements of 4th order.
Rayleigh–Taylor instability: Density map obtained with 512, 1024, 2048 and 4096 cells using a 2nd order Godunov method.
Tracer of fluid advected against a massive and luminous body, performed with FARGO3D+Nested-Meshes.






